一、基本要求
构建一个N*N的从左上角到右下角的随机迷宫,然后在这一迷宫上寻找迷宫路径。
二、需求描述
1. 问题描述
构建一个N*N的从左上角到右下角的随机迷宫,然后在这一迷宫上寻找迷宫路径。该设计一共包括如下三个部分:
①构建随机迷宫
②寻找迷宫路径,使用非递归形式
2. 基本要求
在生成随机迷宫时,考虑如何使选取墙的次数最少,并使得任意两个方格之间均有路径
3. 输入要求
输入形式:输入随机迷宫的行数和列数
4. 输出要求
输出形式:用图形方式输出随机创建的迷宫及迷宫路径
三、设计
1 结构设计
函数调用关系:
深度优先搜索:
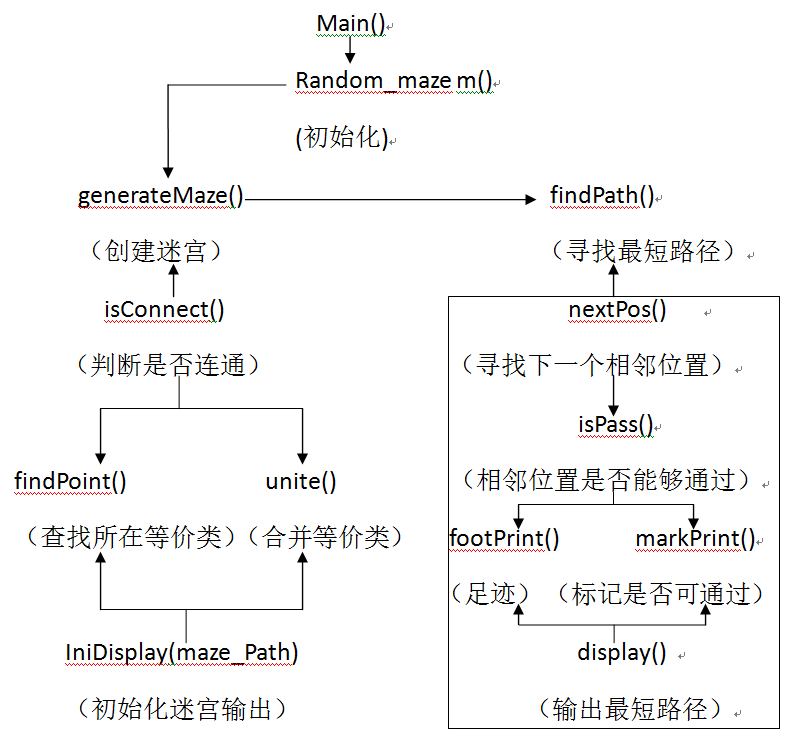
广度优先搜索:
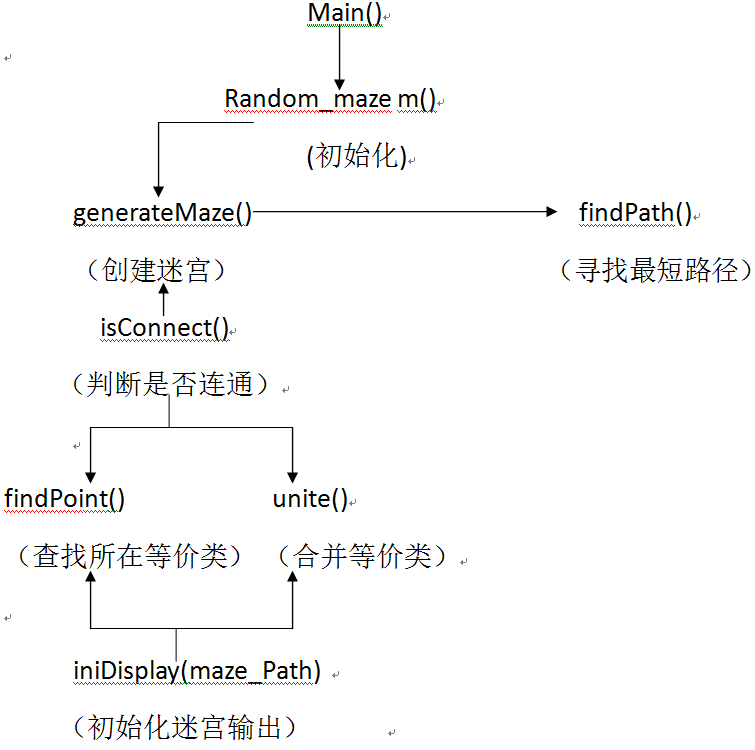
2 数据及数据类(型)定义
方法一、 深度优先搜索:
① 定义迷宫的二维数组中的每个元素都是maze类型
struct maze //存储信息
{
int x,y; //分别表示行列位置s
int direction; //迷宫方向
int state[N]; //迷宫各方向的状态
int flag; //记录在路径中的位置,距出发点的距离
int sign; //是否能通过的标志
int mark; //为了防止重复输出
};
② 定义进行深度优先搜索的栈的结构,栈中元素类型为maze类型
struct mazeStack //栈结构
{
maze *base=0; //栈底指针,在栈构造之前和销毁之后,base的值为NULL
maze *top=0; //栈顶指针
int stackSize=0; //栈的大小
};
③ eq表示等价类,生成迷宫时需要生成该类的对象以调用该类的方法
class eq
{
public:
eq(int number);
int findPoint(int n); //查找根结点(所在等价类)
void unite(int m,int n); //合并等价类
private:
vector<int> s; //表示等价类的数组,记录当前位置
};
④ 生成迷宫的类,通过该类的对象调用创建迷宫和寻找路径的方法
class Random_maze
{
public:
Random_maze(int m,int n);
void generateMaze(); //随机生成迷宫
void findPath(vector<vector<maze> >& m); //寻找路径
void iniDisplay(vector<vector<maze> >& m); //迷宫展示(初始化)
void display(vector<vector<maze> >& m); //迷宫展示(找到路径)
private:
int row,col,conum=0,curstep=0; //迷宫的行和列、当前足迹
mazeStack a,s,t; //s用来寻找路径,t用来保存路径信息
eq *mData; //等价类对象
vector<vector<maze> > mazeMap; //定义迷宫
bool isPass(maze m); //判断当前位置是否可以通过
void footPrint(maze a); //标记当前位置
maze nextPos(maze c,int di); //寻找下一个位置
void markPrint(maze b); //标记为不能通过
bool initStack(mazeStack *s); //初始化空栈
bool push(mazeStack *s,maze e); //压栈
bool isEmpty(mazeStack s); //判空
maze pop(mazeStack s,maze e); //出栈
maze getTop(mazeStack s,maze e); //得到栈顶元素
bool isConnect(maze& m,maze& n); //判断是否连通
};
方法二、广度优先搜索:
① eq表示等价类,生成迷宫时需要生成该类的对象以调用该类的方法
class eq //等价类
{
public:
eq(int number); //初始化
int findPoint(int n); //查找根结点(所在等价类)
void unite(int m,int n); //合并等价类
private:
vector<int> s; //表示等价类的数组,记录当前位置
};
② 定义迷宫的二维数组中的每个元素都是maze类型
struct maze //存储信息
{
int x,y; //分别表示行列位置
int point; //根节点指向
int pos; //当前位置
int sign; //标记该位置是否能通过
int mark; //标记走过的步数并最后标记路径中的点
int footprint; //寻找路径时标记某位置是否已经走过
maze *last; //上一步的坐标
};
③ 生成迷宫的类,通过该类的对象调用创建迷宫和寻找路径的方法
class Random_maze
{
public:
Random_maze(int m,int n); //初始化
void generateMaze(); //随机生成迷宫
void findPath(vector<vector<maze> >& m); //寻找路径
void iniDisplay(vector<vector<maze> >& m); //迷宫展示(初始化)
private:
int row,col,conum=0,curstep=0; //迷宫的行和列、当前足迹
queue<maze*> q; //队列
eq *mData; //等价类对象
vector<vector<maze> > mazeMap; //定义迷宫
bool isConnect(maze& m,maze& n); //判断是否连通
};
3.算法设计及分析(各模块算法及类内函数的算法伪码表示)
深度优先搜索:
1) 初始化
(1)初始化未创建的迷宫信息:
Random_maze::Random_maze(int m,int n):row(m),col(n),mazeMap(m,vector
{
设置行数;
设置列数;
创建一个等价类对象;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
描述行列信息;
迷宫该位置输出标记置0(未输出);
迷宫该位置通过标记置-1(能通过);
迷宫该位置四个方向都设为墙;
}
}
入口左边的墙打开;
出口右边的墙打开;
}
(2)初始化等价类
eq::eq(int numElements) : s(numElements)
{
设置一个一维数组表示等价类集合,并将数组元素全部初始化为-1;
}
2) 创建迷宫:
(1)查找所在等价类
int eq::findPoint(int x)
{
If(该点所在等价类值仍为-1,未合并)
返回当前点;
Else
{
已经合并过,调用findPoint()递归查找当前点的祖先节点,即所在的等价类;
返回所在代表等价类的祖先节点;
}
}
(2)合并所在等价类
void eq::unite(int root1,int root2)
{
If(root1比roo2所在等价类中点的数目少)
{
把root1所在等价类中点加入root2所在等价类中;
将root1的祖先节点指向root2;
}
Else
{
把root2所在等价类中点加入root1所在等价类中;
将root2的祖先节点指向root1;
}
}
(3)判断是否已经连通
bool Random_maze::isConnect(maze& m,maze& n)
{
得到两个点的位置;
If(祖先节点相同)
{
If(均未经过合并)
返回假;
Else
返回真;
}
}
(4)生成函数
void Random_maze::generateMaze()
{
If(迷宫中方格数小于等于四)
退出;
While(1)
{
随机生成一个位置的横纵坐标;
随机选择该位置的一道墙;
Switch(墙)
Case0:
If(是左边界)
退出;
If(当前点和它左边的点在同一个集合)
退出;
else
{
得到当前点的祖先节点;
得到当前点左边点的祖先节点;
将两个点所在的集合合并;
已经开辟的房间数加1;
当前点的左边界打通;
当前点左边点的右边界打通;
}
退出;
Case1:
If(是上边界)
退出;
If(当前点和它上边的点在同一个集合)
退出;
else
{
得到当前点的祖先节点;
得到当前点上边点的祖先节点;
将两个点所在的集合合并;
已经开辟的房间数加1;
当前点的上边界打通;
当前点上边点的下边界打通;
}
退出;
Case2:
If(是右边界)
退出;
If(当前点和它右边的点在同一个集合)
退出;
else
{
得到当前点的祖先节点;
得到当前点右边点的祖先节点;
将两个点所在的集合合并;
已经开辟的房间数加1;
当前点的右边界打通;
当前点右边点的左边界打通;
}
退出;
Case3:
If(是下边界)
退出;
If(当前点和它下边的点在同一个集合)
退出;
else
{
得到当前点的祖先节点;
得到当前点下边点的祖先节点;
将两个点所在的集合合并;
已经开辟的房间数加1;
当前点的下边界打通;
当前点下边点的上边界打通;
}
退出;
}
If(开辟的房间数为矩阵中所有房间的数目)
退出;
}
3) 寻找最短路径
(1)判断是否可以通过
bool Random_maze::isPass(maze m)
{
If(右边可以通行且没有被走过)
{
当前点的通过标记加1;
返回真;
}
Else if(下边可以通行且没有被走过)
{
当前点的方向设为向下;
当前点的通过标记加1;
返回真;
}
Else if(上边可以通行且没有被走过)
{
当前点的方向设为向上;
当前点的通过标记加1;
返回真;
}
Else if(左边可以通行且没有被走过)
{
当前点的方向设为向左;
当前点的通过标记加1;
返回真;
}
Else
返回假,均不能通过;
}
(2)标记足迹
void Random_maze::footPrint(maze a)
{
将当前点的足迹标记为距起点的距离;
}
(3)寻找下一个要走的点
maze Random_maze:: nextPos(maze c,int di)
{
创建一个一维数组保留方向信息;
If(方向向右)
{
If(为右边界)
{
方向改为下;
返回当前位置;
}
Else
{
修改当前位置为当前点右方的位置;
返回当前位置;
}
}
If(方向向下)
{
If(为下边界)
{
方向改为左;
返回当前位置;
}
Else
{
修改当前位置为当前点下方的位置;
返回当前位置;
}
}
If(方向向左)
{
If(为左边界)
{
方向改为上;
返回当前位置;
}
Else
{
修改当前位置为当前点左方的位置;
返回当前位置;
}
}
If(方向向上)
{
If(为上边界)
{
返回当前位置;
}
Else
{
修改当前位置为当前点上方的位置;
返回当前位置;
}
}
返回当前位置;
}
(4)标记当前位置是否能通过
void Random_maze:: markPrint(maze b)
{
标记改为0,表示当前位置已经走过但不能通过;
}
(5)寻找最短路径
void Random_maze::findPath(vector<vector
{
记录初始位置;
初始化栈s;
初始化栈t;
Do
{
If(当前位置可通过)
{
留下足迹;
用一个点e记录当前位置;
到出发点的距离加1;
e的方向为当前位置的方向;
e到起点的距离为当前位置到起点的距离;
将e压入两个栈中;
根据e寻找下一个可以通过的位置;
修改当前位置信息;
If(当前位置为终点)
{
终点到起点的距离即为当前位置到起点的距离;
停止;
}
}
Else
{
标记当前位置已经走过但不能通过;
记录当前位置到起点的距离为0;
将当前位置从两个栈中弹出,返回上一步;
当前位置到起点距离减1;
}
}While(1)
}
4) 输出
(1) 输出初始化迷宫
void Random_maze::iniDisplay(vector<vector
{
上下左右边界均设为墙;
循环输出,如果是上下墙,打通输出“ ”,未打通输出“_”,如果是左右墙,打通输出“ ”,未打通输出“|”;
}
(2) 输出找到路径的迷宫
void Random_maze::display(vector<vector
{
上下左右边界均设为墙;
循环输出,未打通的上下侧边墙保持“_”,在路径中,输出'*',未打通的左右侧边墙保持'|';
借助新建的一个栈将原栈中保留的路径信息输出;
输出栈中元素数目即为走过的步数;
}
广度优先搜索:
1) 初始化
与深度优先搜索基本相同;
2) 创建迷宫
查找所在等价类和合并等价类以及判断是否连通与深度优先搜索相同;
创建迷宫:
void Random_maze::generateMaze()
{
If(迷宫中方格数小于等于四)
退出;
While(1)
{
随机生成一个位置的横纵坐标;
随机选择该位置的一道墙;
If(不是边界,且是真正的要打通的格子)
{
Switch(墙)
Case0:
If(是左边界)
退出;
If(当前点和它左边的格子在同一个集合)
退出;
else
{
得到当前点的祖先节点;
得到当前点左边格子的祖先节点;
将两个格子所在的集合合并;
已经开辟的房间数加1;
当前格子标记为打通;
当前格子左边的格子打通;
二者之间的格子标记为打通;
}
退出;
Case1:
If(是上边界)
退出;
If(当前点和它上边的格子在同一个集合)
退出;
else
{
得到当前格子的祖先节点;
得到当前点上边格子的祖先节点;
将两个格子所在的集合合并;
已经开辟的房间数加1;
当前格子打通;
当前格子上边的格子打通;
二者之间的格子标记为打通;
}
退出;
Case2:
If(是右边界)
退出;
If(当前点和它右边的格子在同一个集合)
退出;
else
{
得到当前格子的祖先节点;
得到当前点右边格子的祖先节点;
将两个格子所在的集合合并;
已经开辟的房间数加1;
当前格子1打通;
当前格子右边的格子打通;
二者之间的格子标记为打通;
}
退出;
Case3:
If(是下边界)
退出;
If(当前点和它下边的格子在同一个集合)
退出;
else
{
得到当前格子的祖先节点;
得到当前格子下边点的祖先节点;
将两个格子所在的集合合并;
已经开辟的房间数加1;
当前格子打通;
当前格子下边的格子打通;
二者之间的格子标记为打通;
}
退出;
}
If(开辟的房间数为矩阵中真正应该连通的所有所有格子的数目)
退出;
}
3) 查找并输出最短路径
void Random_maze::findPath(vector<vector
{
记录起点和终点;
将起点的上一个点设为它自身;
将起点加入队列中;
设置起点标记,步数为1;
创建一个一维数组保留方向信息;
While(队列不为空)
{
得到队首元素;
弹出队首元素;
If(到达终点)
{
根据mark标记输出行走的步数;
将当前格子标记为在路径中;
增加一个指针;
获取当前位置的前一个位置;
While(前一个位置不是起点)
{
If(两个位置横坐标或纵坐标相差1)
标记前一个位置在路径中;
将前一个位置设置为当前位置;
}
停止;
}
Else
{
在四个方向寻找可达的相邻位置:
If(要寻找的点是边界){ }
Else
{
得到相邻位置的坐标;
If(相邻位置可达)
{
将该可达的相邻位置放入队列;
将该位置标记为已走过;
所有可达的相邻位置标记加1;
}
}
}
}
循环输出,起点和终点输出“★”,如果未打通,输出“■”,在路径中输出“☆”,否则输出“ ”;
}
4) 初始化迷宫输出
void Random_maze::iniDisplay(vector<vector
{
循环输出,起点和终点输出“★”,如果未打通,输出“■”,否则输出“ ”;
}
四、实验结果
1.示例图
“广度优先搜索+剪枝”:
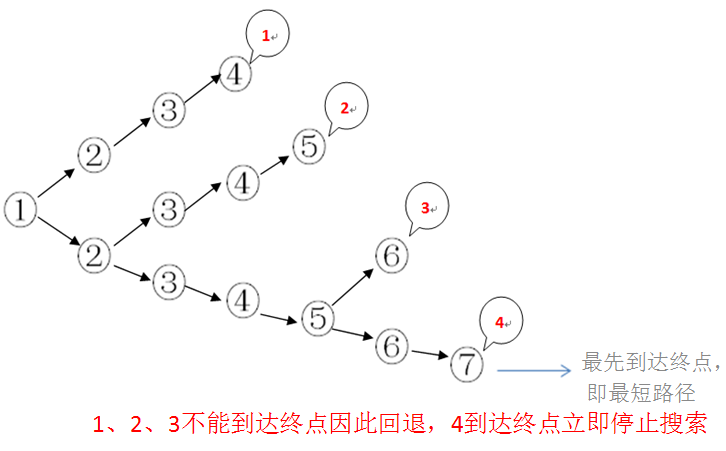
链式队列示意图:
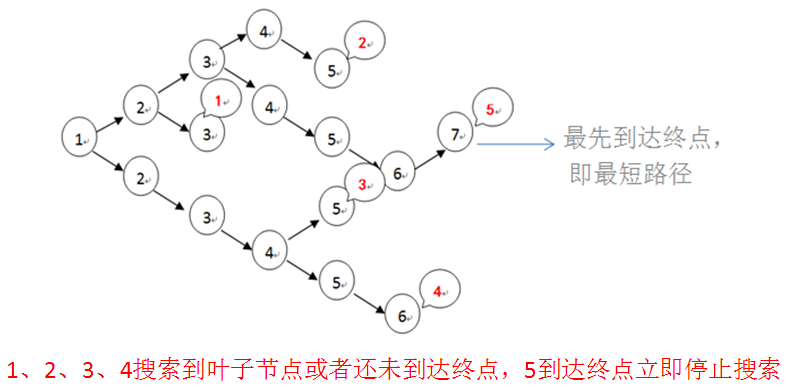
2. 测试结果
输入:
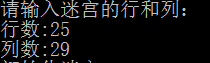
输出:
方法一(深度优先):



方法二(广度优先):


五、分析与探讨
创建迷宫:
用等价类随机创建迷宫,首先将所有的方格都当作一个单独的类,当将两个方格之间的墙打通时,将两个等价类合并。将所有的方格先各自看作一棵只有一个节点的树,整个迷宫就是许多树构成的森林,当把相邻两个方格打通时,将其代表的树合并成一棵,直到树中节点的个数为整个迷宫中点的数目,将整个森林变成一棵树,生成了一个迷宫图的生成树。
在随机创建迷宫时,为了使得任意两个放格之间均有路径可达,将每个方格看作一个节点,即得到一棵能够包含所有节点的生成树,同时为了能使选取墙的次数最少,就要保证得到的是一棵最小生成树,得到最小生成树的方法很多,我在写课设的时候选取了随机prim算法进行迷宫生成,因为相比深度、广度优先搜索,随机prim算法生成的迷宫岔路多,自然而又复杂。
随机prim算法的核心是:
1、让迷宫全是墙
2、随机选一个格作为迷宫的通路,然后把它的邻墙放入列表
3、当列表里还有墙时
3.1.从列表里随机选一个墙,如果它对面的格子不是迷宫的通路
1)把墙打通,让对面的格子成为迷宫的通路
2)把那个格子的邻墙加入列表
3.2.如果对面的格子已经是通路了,那就从列表里移除这面墙
另:
广度优先搜索用方格代表墙,因此为了能够将迷宫表示出来,需要将迷宫扩展成为[2row+1][2col+1]大小,[2i+1][2j+1]是真正的要打通的所有位置;
先将所有格子都设为不通,为迷宫设置一圈墙,随机选取一个点作为起点,当它向某一个方向开通路时,将它与该方向的相邻格子以及二者之间的格子设为可通过;
继续随机选取,直到任意两点之间都能够可达,即最终合并后的起点所在的等价类中元素数目为((row-1)/2)*((col-1)/2).
寻找迷宫最短路径:
方法一:回溯法——深度优先搜索(栈)
深度优先搜索采用“先进后出”的栈结构,从起点出发,寻找相邻连通位置,入栈,从栈中取出一个继续执行该操作,若不可继续走,则从栈中拿出该位置,栈不为空就继续执行,直至首次到达终点,将栈中的元素逆向pop可得到最短路径
能够使用回溯法得到最短路径的原因:由于创建迷宫时是生成一棵生成树,因此,从起点到终点的路径即为根节点到起点和终点连通的一条路,只有一条,只要保证不经过额外的分支节点即可得到最短路径
方法二:分支限界单源最短路径算法——“广度优先搜索加剪枝”(链式队列)
分支限界单源最短路径算法(此处认为每条边权重均为1,权重之和最小即边数最少,路径最短)主要思想是广度优先搜索,只不过在搜索过程中如果经判断可知不能到达终点或者不能以最优解到达终点,则需要将这条路从最短路径选择中排除,最后到达终点立即停止,不再遍历。此时没有在终点所在的链表上的点都被排除,只剩下一条最短路径。
1.从标记0的起点出发,寻找所有相邻连通位置(儿子结点),入队列并标记1,可构成多条分支链,每找到一个相邻位置就挂一个节点、记录上个节点并将标记加1
2.若这些位置不能到达终点或不是最优解,将之从队列中删除,并排除这条分支链(剪枝)
3.从队列中pop出一个位置,继续以同样的方法向前走,直到到达终点或者活节点表为空为止
4.从终点所在的链输出,得到最短路径
因为是一层一层遍历,到终点立即停止,因此最后得到的路径一定是经过位置最少的,即最短路径。
补充算法: A*算法
A算法是一种启发式搜索,可看做广度优先搜索和迪杰斯特拉算法的发展。A算法相对广度优先搜索算法,除了考虑中间某个点同出发点的距离以外,还考虑了这个点同目标点的距离。保证找到最短路径(最优解的)条件,关键在于估价函数f(n)的选取(或者说h(n)的选取)估价函数取得越好,距离估计与实际值越接近。
A算法是一个可采纳的最好优先算法。A算法的估价函数可表示为:
f’(n) = g’(n) + h’(n)
这里,f’(n)是估价函数,g’(n)是起点到节点n的最短路径值,h’(n)是n到目标的最短路经的启发值。由于这个f’(n)其实是无法预先知道的,所以用估价函数f(n)做近似。g(n)代替g’(n),h(n)代替h’(n),但只有满足h(n)<=h’(n)才行。可以证明应用这样的估价函数是可以找到最短路径的,也就是可采纳的。我们说应用这种估价函数的最好优先算法就是A*算法。
A*算法步骤:
f = g +h
这里:
g= 从起点沿着产生的路径,移动到指定方格的移动耗费。
h = 从那个方格移动到终点的预估移动耗费
1.选择一个合适的估值函数,将起点先添加到开启列表中
2.开启列表中有节点的话,取出第一个节点,即最小f值的节点,
判断此节点是否是目标点,是则找到了,跳出;
根据此节点取得四个方向的节点,求出g,h,f值;
判断每个节点在地图中是否能通过,不能通过则加入关闭列表中,跳出;
判断每个节点是否在关闭列表中,在则跳出;
判断每个节点是否在开启列表中,在则更新g值,f值,还更新其父节点;不在则将其添加到开启列表中,计算g值,h值,f值,添加其节点。
3.把此节点从开启列表中删除,再添加到关闭列表中;
4.把开启列表中按照f值最小的节点进行排序,最小的f值在第一个;
5.重复2,3,4步骤,直到目标点在开启列表中,即找到了;目标点不在开启列表中,开启列表为空,即没找到
在寻找迷宫最短路径问题中可以简单计算 (|x2-x1|+|y2-y1|)*10从而得到当前位置到终点距离的估计值,从而找到估值最小即优先级最高的位置,加入到open表中,继续此过程直至目标点在open列表中。
更多代码访问:http://qiongli97.github.io
转载请注明来源